.ipynb .pdf

Binder Live Code

Contents

MgNet: a special CNN based on multigrid method

-->

Please access the video via one of the following two ways

1. Google Drive: https://drive.google.com/drive/folders/1x5fREf1-WZEoyR2ceMV9JYxuZPLACFwj?usp=share_link

2. Baidu Netdisk: https://pan.baidu.com/s/1U2Asok8HJwqqjp6S0JhLWw?pwd=mrgl

Download the lecture notes here: Notes

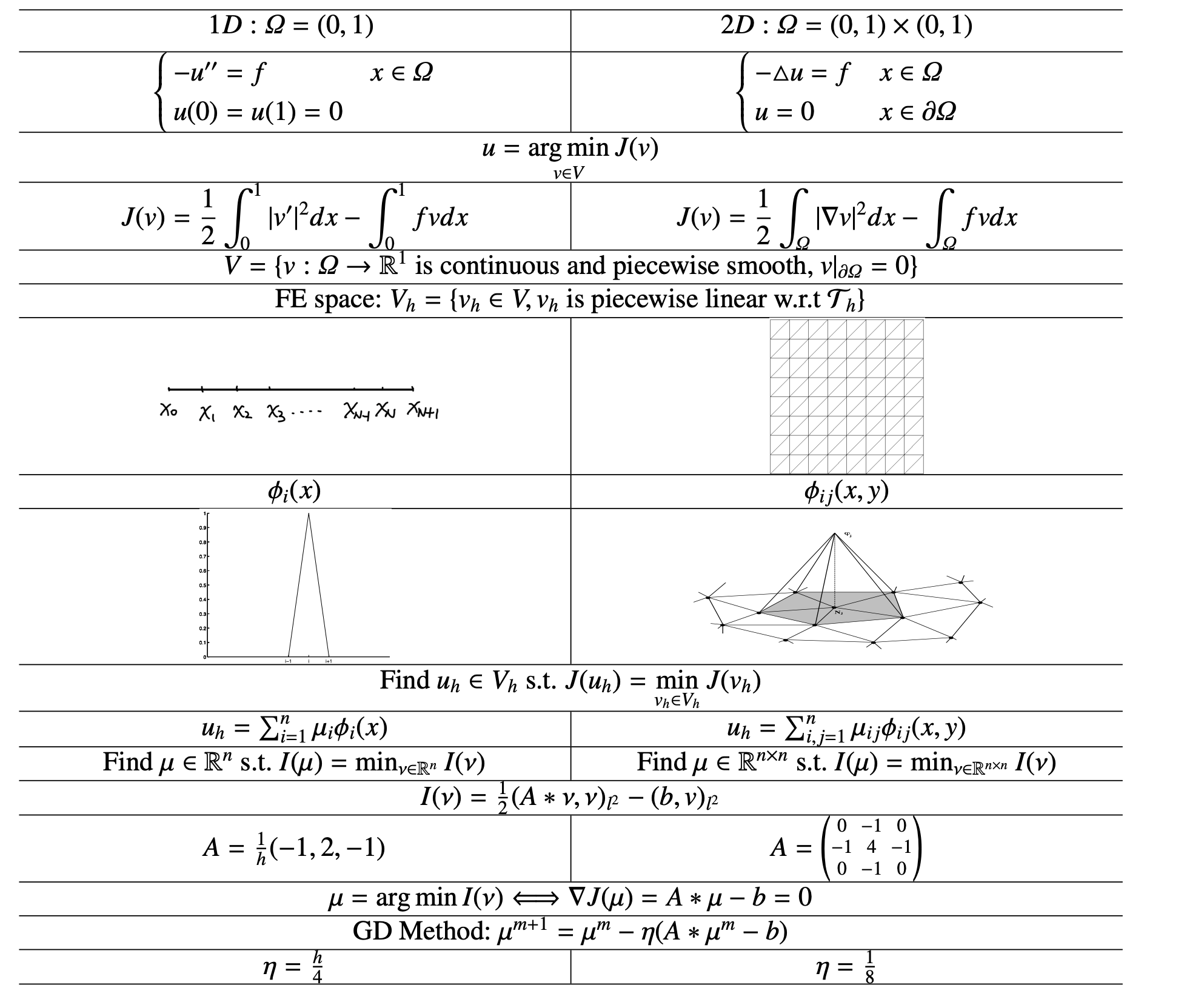
1D and 2D Finite Element and Multigrid

1D and 2D Comparison for Finite Element and Multigrid

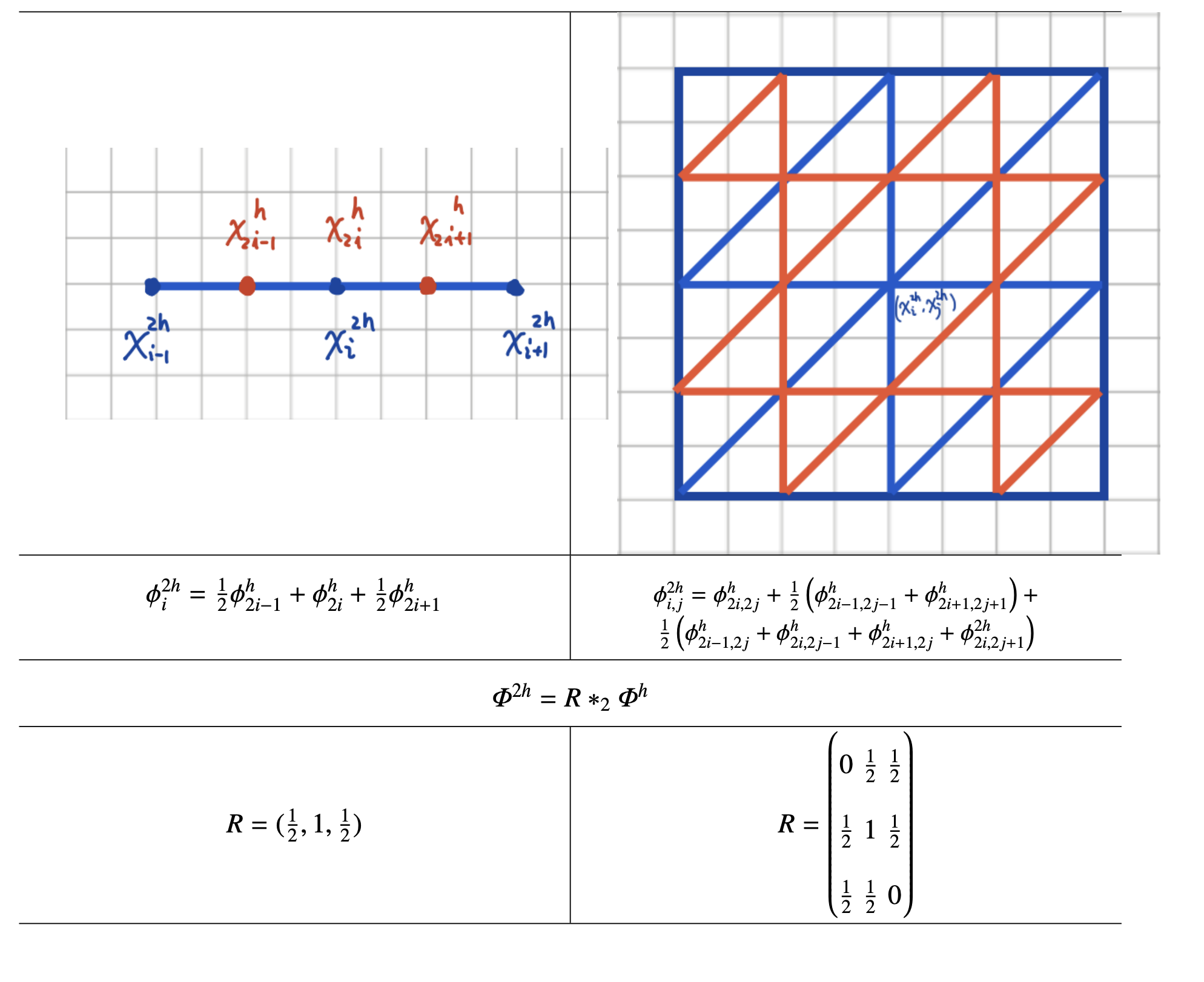
Basic multigrid components

Multigrid algorithm for \(A * \mu=f\)

Algorithm 10 (A multigrid algorithm \(\mu=\operatorname{MG} 1\left(f ; \mu^{0} ; J, v_{1}, \cdots, v_{J}\right)\))

Set up:

\[ f^{1}=f, \quad \mu^{1}=\mu^{0} \]

Smoothing and restriction from fine to coarse level (nested)

For \(\ell=1: J\) do

For \(i=1: v_{\ell}\) do

\[ \mu^{\ell} \leftarrow \mu^{\ell}+S^{\ell} *\left(f^{\ell}-A_{\ell} * \mu^{\ell}\right) \]

EndFor

Form restricted residual and set initial guess:

\[ \mu^{\ell+1} \leftarrow \Pi_{\ell}^{\ell+1} \mu^{\ell}, \quad f^{\ell+1} \leftarrow R *_{2}\left(f^{\ell}-A_{\ell} * \mu^{\ell}\right)+A_{\ell+1} * \mu^{\ell+1} \]

EndFor

Prolongation and restriction from coarse to fine level

For \(\ell=J-1: 1\) do

\[ \mu^{\ell} \leftarrow \mu^{\ell}+R *_{2}^{\top}\left(\mu^{\ell+1}-\Pi_{\ell}^{\ell+1} \mu^{\ell}\right) \]

EndFor

\[ \mu \leftarrow \mu^{1} \]

Remark

The above multigrid method for the linear problem \(A * \mu=b\) is independent of the choice of the interpolation operation \(\Pi_{\ell}^{\ell+1}: \mathbb{R}^{n_{\ell} \times n_{\ell}} \mapsto \mathbb{R}^{n_{\ell+1} \times n_{\ell+1}}\) and in particular, we could take \(\Pi_{\ell}^{\ell+1}:=0\). But such an operation is critical for nonlinear problems.

MgNet

Algorithm 11 (\(\mu^{J}=\operatorname{MgNet} 1\left(f ; \mu^{0} ; J, v_{1}, \cdots, v_{J}\right)\))

Set up:

\[ \qquad f^{1}=\theta * f, \quad \mu^{1}=\mu^{0} \]

Smoothing and restriction from fine to coarse level (nested)

For \(\ell=1: J\) do

\(\quad\)

For \(i=1: v_{\ell}\) do

\[ \quad \mu^{\ell} \leftarrow \mu^{\ell}+\sigma \circ S^{\ell} * \sigma \circ\left(f^{\ell}-A_{\ell} * \mu^{\ell}\right) \]

EndFor

Form restricted residual and set initial guess:

\[ \quad \mu^{\ell+1} \leftarrow \Pi_{\ell}^{\ell+1} \mu^{\ell}, \quad f^{\ell+1} \leftarrow R *_{2}\left(f^{\ell}-A_{\ell} * \mu^{\ell}\right)+A_{\ell+1} * \mu^{\ell+1} \]

EndFor