Contents

Polynomials and Weierstrass theorem

-->

Please access the video via one of the following two ways

Download the lecture notes here: Notes

Approximation by polynomials and Weierstrass Theorem

Let \(\alpha=\left(\alpha_{1}, \cdots, \alpha_{d}\right)\) with \(\alpha_{i}\) being non-negative integers, we note \(|\alpha|=\sum_{i=1}^{d} \alpha_{i}\) and

\[ x^{\alpha}=x_{1}^{\alpha_{1}} x_{2}^{\alpha_{2}} \cdots x_{d}^{\alpha_{d}} \]

We use \(\mathbb{P}_{m}\left(\mathbb{R}^{d}\right)\) to define the polynomials of \(d\)-variables of degree less than \(m\) which consists functions of the form

\[ \sum_{|\alpha| \leq m} a_{\alpha} x^{\alpha}=\sum_{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{d} \leq m} a_{\alpha_{1}, \ldots, \alpha_{d}} x_{1}^{\alpha_{1}} x_{2}^{\alpha_{2}} \cdots x_{d}^{\alpha_{d}} \]

Weierstrass Theorem and Proof

Important property: polynomials can approximate any reasonable function!

  • dense in \(C(\Omega)\) [Weierstrass theorem]

  • dense in all Sobolev spaces: \(L^{2}(\Omega), W^{m, p}(\Omega), \ldots\)

Theorem 4

Let \(\Omega \subset R^{n}\) be a closed and bounded set. Given any continuous function \(f(x)\) on \(\Omega\), there exists a sequence of polynomials \(\left\{P_{n}(x)\right\}\) such that

\[ \lim _{n \rightarrow \infty} \max _{x \in \Omega}\left|f(x)-P_{n}(x)\right|=0 \]

Proof. Let us first give the proof for \(d=1\) and \(\Omega=[0,1] .\) Given \(f:[0,1] \rightarrow R\) be a continuous function.

Let

\[ \tilde{f}(x)=f(x)-l(x) \]

where \(l(x)=f(0)+x(f(1)-f(0))\). Then \(\tilde{f}(0)=\tilde{f}(1)=0\). Noting that \(l(x)\) is a linear function, hence without lose of generality, we can only consider the case \(f:[0,1] \rightarrow R\) with \(f(0)=f(1)=0\)

Since \(f\) is continuous on the closed interval \([0,1]\), then \(f\) is uniformly continuous on \([0,1]\).

First we extend \(f\) to be zero outside of \([0,1]\) and obtain \(f: R \rightarrow R\), then it is obviously that \(f\) is still uniformly continuous.

Next for \(0 \leq x \leq 1\), we construct

\[ p_{n}(x)=\int_{-1}^{1} f(x+t) Q_{n}(t) d t=\int_{-x}^{1-x} f(x+t) Q_{n}(t) d t=\int_{0}^{1} f(t) Q_{n}(t-x) d t \]

where \(Q_{n}(x)=c_{n}\left(1-x^{2}\right)^{n}\) and

\[ \int_{-1}^{1} Q_{n}(x) d x=1 \]

Thus \(\left\{p_{n}(x)\right\}\) is a sequence of polynomials.

Since

\[\begin{split} \begin{aligned} \int_{-1}^{1}\left(1-x^{2}\right)^{n} d x &=2 \int_{0}^{1}\left(1-x^{2}\right)^{n} d x=2 \int_{0}^{1}(1-x)^{n}(1+x)^{n} d x \\ & \geq 2 \int_{0}^{1}(1-x)^{n} d x=\frac{2}{n+1}>\frac{1}{n} \end{aligned} \end{split}\]

Combing with \(\int_{-1}^{1} Q_{n}(x) d x=1\), we obtain \(c_{n}<n\) implying that for any \(\delta>0\)

\[ 0 \leq Q_{n}(x) \leq n\left(1-\delta^{2}\right)^{n} \quad(\delta \leq|x| \leq 1) \]

so that \(Q_{n} \rightarrow 0\) uniformly in \(\delta \leq|x| \leq 1\) as \(n \rightarrow \infty\).

Given any \(\epsilon>0\), since \(f\) in uniformly continuous, there exists \(\delta>0\) such that for any \(|y-x|<\delta\), we have

\[ |f(y)-f(x)|<\frac{\epsilon}{2} \]

Finally, let \(M=\max |f(x)|\), using \((1.8),(1.4)\) and \((1.7)\), we have

\[\begin{split} \begin{aligned} \left|p_{n}(x)-f(x)\right| &=\left|\int_{-1}^{1}(f(x+t)-f(t)) Q_{n}(t) d t\right| \leq \int_{-1}^{1}|f(x+t)-f(t)| Q_{n}(t) d t \\ & \leq 2 M \int_{-1}^{-\delta} Q_{n}(t) d t+\frac{\epsilon}{2} \int_{-\delta}^{\delta} Q_{n}(t) d t+2 M \int_{\delta}^{1} Q_{n}(t) d t \\ & \leq 4 M n\left(1-\delta^{2}\right)^{n}+\frac{\epsilon}{2}<\epsilon \end{aligned} \end{split}\]

for all large enough \(n\), which proves the theorem.

The above proof generalize the high dimensional case easily. We consider the case that

\[ \Omega=[0,1]^{d} \]

By extension and using cut off function, W.L.O.G. that we assume that \(f=0\) on the boundary of \(\Omega\) and we then extending this function to be zero outside of \(\Omega\).

Let us consider the special polynomial functions

\[ Q_{n}(x)=c_{n} \prod_{k=1}^{d}\left(1-x_{k}^{2}\right) \]

Similar proof can then be applied. \(\square\)

Curse of dimensionality

Number of coefficients for polynomials of degrees \(n\) in \(\mathbb{R}^{d}\) is

\[\begin{split} N=\left(\begin{array}{c} d+n \\ n \end{array}\right)=\frac{(n+d) !}{d ! n !} \end{split}\]

For example \(n=100\) :

d=

2

4

8

N=

\(5 \times 10^3\)

\(4.6 \times 10^{6}\)

\(3.5 \times 10^{11}\)

Runge’s phenomenon

Consider the case where one desires to interpolate through \(n+1\) equispaced points of a function \(f(x)\) using the n-degree polynomial \(P_{n}(x)\) that passes through those points. Naturally, one might expect from Weierstrass’ theorem that using more points would lead to a more accurate reconstruction of \(f(x)\). However, this particular set of polynomial functions \(P_{n}(x)\) is not guaranteed to have the property of uniform convergence; the theorem only states that a set of polynomial functions exists, without providing a general method of finding one.

The \(P_{n}(x)\) produced in this manner may in fact diverge away from \(f(x)\) as \(\mathrm{n}\) increases; this typically occurs in an oscillating pattern that magnifies near the ends of the interpolation points. This phenomenon is attributed to Runge.

Problem: Consider the Runge function

\[ f(x)=\frac{1}{1+25 x^{2}} \]

(a scaled version of the Witch of Agnesi). Runge found that if this function is interpolated at equidistant points \(x_{i}\) between \(-1\) and 1 such that:

\[ x_{i}=\frac{2 i}{n}-1, \quad i \in\{0,1, \ldots, n\} \]

with a polynomial \(P_{n}(x)\) of degree \(\leq n\), the resulting interpolation oscillates toward the ends of the interval, i.e. close to \(-1\) and 1. It can even be proven that the interpolation error increases (without bound) when the degree of the polynomial is increased:

\[ \lim _{n \rightarrow \infty}\left(\max _{-1 \leq x \leq 1}\left|f(x)-P_{n}(x)\right|\right)=+\infty \]

This shows that high-degree polynomial interpolation at equidistant points can be troublesome

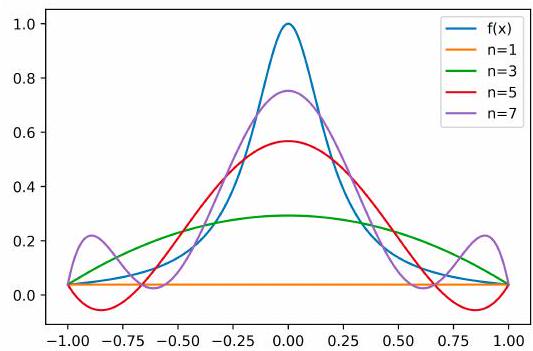
image

Fig. Runge’s phenomenon: Runge function \(f(x)=\frac{1}{1+25 x^{2}}\) and its polynomial interpolation \(P_{n}(x)\).