Contents

Linearly separable sets

from IPython.display import IFrame

IFrame(src="https://cdnapisec.kaltura.com/p/2356971/sp/235697100/embedIframeJs/uiconf_id/41416911/partner_id/2356971?iframeembed=true&playerId=kaltura_player&entry_id=1_3im0zbc7&flashvars[streamerType]=auto&flashvars[localizationCode]=en&flashvars[leadWithHTML5]=true&flashvars[sideBarContainer.plugin]=true&flashvars[sideBarContainer.position]=left&flashvars[sideBarContainer.clickToClose]=true&flashvars[chapters.plugin]=true&flashvars[chapters.layout]=vertical&flashvars[chapters.thumbnailRotator]=false&flashvars[streamSelector.plugin]=true&flashvars[EmbedPlayer.SpinnerTarget]=videoHolder&flashvars[dualScreen.plugin]=true&flashvars[hotspots.plugin]=1&flashvars[Kaltura.addCrossoriginToIframe]=true&&wid=1_3sj1s85k" ,width='800', height='500')
-->

Please access the video via one of the following two ways

IFrame(src="https://cdnapisec.kaltura.com/p/2356971/sp/235697100/embedIframeJs/uiconf_id/41416911/partner_id/2356971?iframeembed=true&playerId=kaltura_player&entry_id=1_awemnq71&flashvars[streamerType]=auto&flashvars[localizationCode]=en&flashvars[leadWithHTML5]=true&flashvars[sideBarContainer.plugin]=true&flashvars[sideBarContainer.position]=left&flashvars[sideBarContainer.clickToClose]=true&flashvars[chapters.plugin]=true&flashvars[chapters.layout]=vertical&flashvars[chapters.thumbnailRotator]=false&flashvars[streamSelector.plugin]=true&flashvars[EmbedPlayer.SpinnerTarget]=videoHolder&flashvars[dualScreen.plugin]=true&flashvars[hotspots.plugin]=1&flashvars[Kaltura.addCrossoriginToIframe]=true&&wid=1_tiw3d9xz"  ,width='800', height='500')
-->

Download the lecture notes here: Notes

Definition of linearly separable sets

In this section, we consider a special class of \(k\) linearly separable sets for \(k\ge 2\). Let us first introduce the following definition for binary classification.

For \(k=2\), there is a very simple geometric interpretation of two linearly separable sets.

Definition

The two sets \(A_1\), \(A_2\subset \mathbb{R}^d\) are linearly separable if there exists a hyperplane

such that \(wx+b>0\) if \(x \in A_1\) and \(wx+b<0\) if \(x \in A_2\)

(1)\[ H_{0}=\{x:wx+b=0\} \]
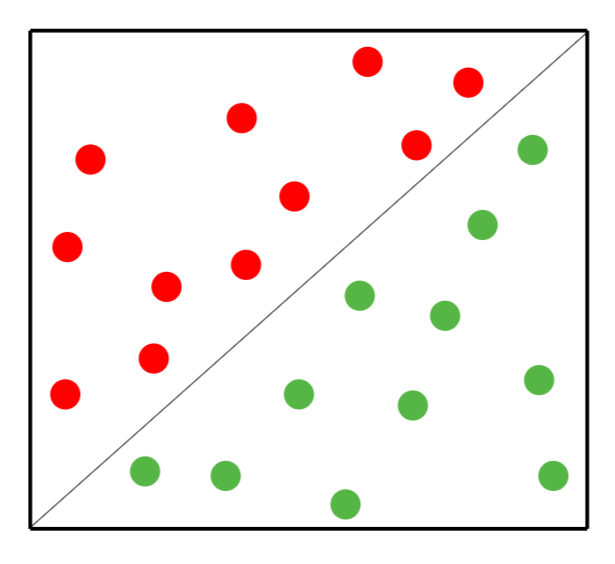
../_images/LinearS1.png

Fig. 1 One linearly separable set

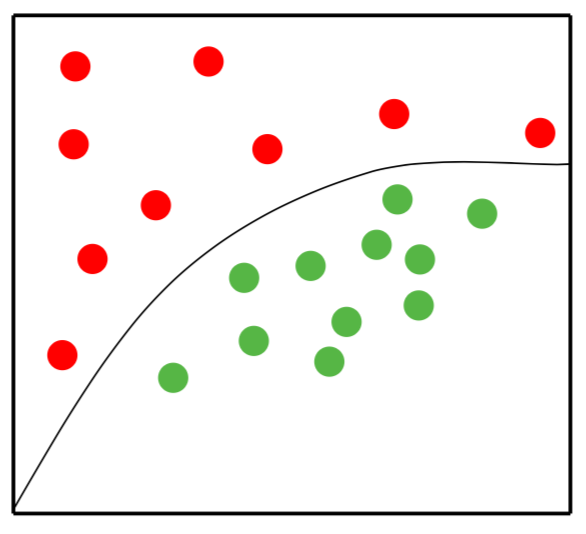
../_images/NLinearS1.png

Fig. 2 Non-linearly separable set

Lemma

The two sets \(A_1\), \(A_2\subset \mathbb{R}^d\) are linearly separable if there exists

(2)\[\begin{split} W= \begin{pmatrix} w_1\\ w_2 \end{pmatrix} \in \mathbb{R}^{2\times d}, b= \begin{pmatrix} b_1\\ b_2 \end{pmatrix} \in \mathbb{R}^{2\times d} \end{split}\]

such that

(3)\[ w_1x+b_1 > w_{2} x+b_2,\ \forall x\in A_1, \]

and

(4)\[ w_1x+b_1 < w_2 x+b_2,\ \forall x\in A_2. \]

Proof

Proof. Here, we can just take \(w = w_1 - w_2\) and \(b = b_1 - b_2\), then we can check that the hyperplane \(wx + b\) satisfies the definition as presented before.◻

Now let us consider multi-class classification. To begin with the definition, let us assume that the data space is divided into \(k\) classes represented by \(k\) disjoint sets \(A_1,A_2,\cdots,A_k\subset \mathbb{R}^d\), which means

\[ A = A_1\cup A_2\cup \cdots \cup A_k, ~A_i\cap A_j = \emptyset, \forall i \neq j \]

Definition

A collection of subsets \(A_1,...,A_k\subset \mathbb{R}^d\) are linearly separable if there exist

(5)\[\begin{split} W= \begin{pmatrix} w_1\\ \vdots\\ w_k \end{pmatrix} \in \mathbb{R}^{k\times d}, b= \begin{pmatrix} b_1\\ \vdots\\ b_k \end{pmatrix} \in \mathbb{R}^{k\times d} \end{split}\]

such that, for each \(1\le i\le k\) and \(j \neq i\)

(6)\[ w_ix+b_i > w_jx+b_j,\ \forall x\in A_i \]

namely, each pairs of \(A_i\) and \(A_j\) are linearly separable by the plane

(7)\[ H_{ij}=\{(w_i-w_j)\cdot x+(b_i-b_j) = 0\}, \quad \forall j\neq i \]

The geometric interpretation for linearly separable sets is less obvious when \(k>2\).

Lemma

\(A_1,...,A_k\) are linearly separable and \(W\in \mathbb{R}^{k\times d}\) and \(b\in\mathbb{R}^k\) satisfy (5). Define

(8)\[ \Gamma_i(W,b) = \{x\in\mathbb R^d: (Wx+b)_i > (Wx+b)_j,\ \forall j \neq i\} \]

Then for each \(i\),

(9)\[ A_i \subset \Gamma_i(W,b) \]

We note that each \(\Gamma_i(W,b)\) is a polygon whose boundary consists of hyperplanes given by (7).

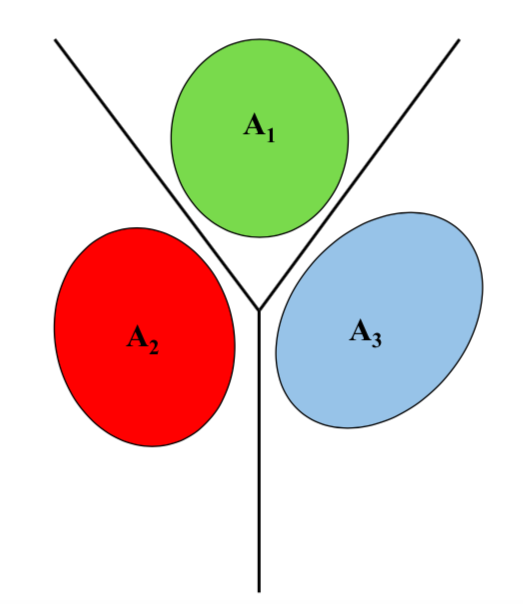
../_images/3-class.png

Fig. 3 Linearly separable sets in 2-d space (k = 3)

We next introduce two more definitions of linearly separable sets that have more clear geometric interpretation.

Definition

A collection of subsets \(A_1,...,A_k\subset \mathbb{R}^d\) is all-vs-one linearly separable if for each \(i = 1,...,k\), \(A_i\) and \(\displaystyle \cup_{j\neq i} A_j\) are linearly separable.

../_images/MulLClassfication.PNG

Fig. 4 All-vs-One linearly separable sets (k = 3)

Definition

A collection of subsets \(A_1,...,A_k\subset \mathbb{R}^d\) is pairwise linearly separable if for each pair of indices \(1\leq i < j\leq k\), \(A_i\) and \(A_j\) are linearly separable.

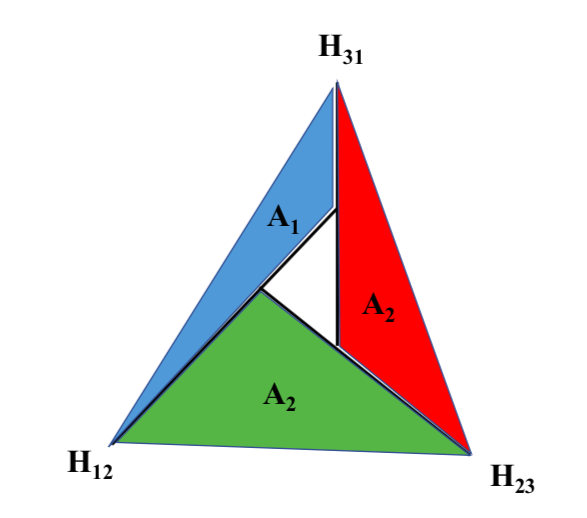
../_images/pairwise_linearly_separable.png

Fig. 5 Pairwise linearly separable sets in 2-d space (k =3)

We begin by comparing our notion of linearly separable to the two other previously introduced geometric definitions of all-vs-one linearly separable and pairwise lineaerly separable. Obviously, in the case of two classes, they are all equivalent, however, with more than two classes this is no longer the case. We do have the following implications, though.

Lemma

If \(A_1,...,A_k\subset \mathbb{R}^d\) are all-vs-one linearly separable, then they are linearly separable as well.

Proof

Proof. Assume that \(A_1,...,A_k\) are all-vs-one linearly separable. For each \(i\), let \(w_i\), \(b_i\) be such that \(w_ix + b_i\) separates \(A_i\) from \(\cup_{j\neq i} A_j\), i.e. \(w_ix + b_i > 0\) for \(x\in A_i\) and \(w_ix + b_i < 0\) for \(x \in \cup_{j\neq i} A_j\).

Set \(W = (w_1^T,w_2^T,\cdots,w_k^T)^T\), \(b = (b_1,b_2,\cdots,b_k)^T\) and observe that if \(x\in A_i\), then \((Wx + b)_i > 0\) while \((Wx + b)_j < 0\) for all \(j\neq i\).◻

Lemma

If \(A_1,...,A_k\subset \mathbb{R}^n\) are linearly separable, then they are pairwise linearly separable as well.

Proof

Proof. If \(A_1,...,A_k\subset \mathbb{R}^d\) are linearly separable, suppose that \(W = (w_1^T,w_2^T,\cdots,w_k^T)^T\), \(b = (b_1,b_2,\cdots,b_k)^T\). So we have

\[\begin{split} \begin{cases} w_i x+ b_i > w_j x + b_j & x\in A_i \\ w_i x+ b_i < w_j x + b_j& x\in A_j \\ \end{cases} \end{split}\]

Take \(w_{i,j} = w_i - w_j, b_{i,j} = b_i-b_j\), then we have

\[\begin{split} w_{i,j}x + b_{i,j}\begin{cases} > 0 & x\in A_i \\ < 0 & x\in A_j \\ \end{cases} \end{split}\]

So \(A_1,...,A_k\) are pairwise linearly separable.◻

However, the converses of both of these statements are false, as the following examples show.

Example

Consider the sets \(A_1, A_2, A_3\subset \mathbb{R}\) given by \(A_1 = [-4,-2]\), \(A_2 = [-1,1]\), and \(A_3 = [2,4]\). These sets are clearly not one-vs-all linearly separable because \(A_2\) cannot be separated from both \(A_1\) and \(A_3\) by a single plane (in \(\mathbb{R}\) this is just cutting the real line at a given number, and \(A_2\) is in the middle).

However, these sets are linearly separated by \(W = [-2,0,2]^T\) and \(b = [-3,0,-3]^T\), for example.

Example

Consider the sets \(A_1, A_2, A_3\subset \mathbb{R}^2\) shown in figure Fig. 5. Note that \(A_i\) and \(A_j\) are separated by hyperplane \(H_{i,j}\) (drawn in the figure) and so these sets are pairwise linearly separable. We will show that they are not linearly separable.

Assume to the contrary that \(W\in \mathbb{R}^{3\times 2}\) and \(b\in \mathbb{R}^2\) separate \(A_1\), \(A_2\), and \(A_3\). Then \((w_i - w_j)x + (b_i - b_j)\) must be a plane which separates \(A_i\) and \(A_j\). Now consider a point \(z\) bounded by \(A_1\), \(A_2\) and \(A_3\) in figure Fig. 5. We see from the figure that given any plane separating \(A_1\) from \(A_2\), \(z\) must be on the same side as \(A_2\), given any plane separating \(A_2\) from \(A_3\), \(z\) must be on the same side as \(A_3\), and given any plane separating \(A_3\) from \(A_1\), \(z\) must be on the same side as \(A_1\).

This means that \((w_2 - w_1)z + (b_2 - b_1) > 0\), \((w_3 - w_2)z + (b_3 - b_2) > 0\), and \((w_1 - w_3)z + (b_1 - b_3) > 0\). Adding these together, we obtain \(0 > 0\), a contradiction.

The essence behind this example is that although the sets \(A_1\), \(A_2\), and \(A_3\) are pairwise linearly separable, no possible pairwise separation allows us to consistently classify arbitrary new points. However, a linear separation would give us a consistent scheme for classifying new points.

So the notion of linear separability is sandwiched in between the more intuitive notions of all-vs-one and pairwise separability. It turns out that linear separability is the notion which is most useful for the \(k\)-class classification problem and so we focus on this notion of separability from now on.