Contents

Convex functions and convergence of gradient descen

--> -->

Please access the video via one of the following two ways

Download the lecture notes here: Notes

Convex functions and convergence of gradient descent

Convex function

Then, let us first give the definition of convex sets.

Definition 1 (Convex set)

A set \(C\) is convex, if the line segment between any two points in \(C\) lies in \(C\), i.e., if any \(x, y \in C\) and any \(\alpha\) with \(0 \leq \alpha \leq 1\), there holds

\[ \alpha x+(1-\alpha) y \in C \]

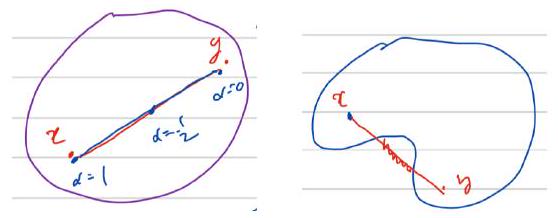
Here are two diagrams for this definition about convex and non-convex sets. image

Following the definition of convex set, we define convex function as following.

Definition 2 (Convex function)

Let \(C \subset \mathbb{R}^{n}\) be a convex set and \(f: C \rightarrow \mathbb{R}\) :

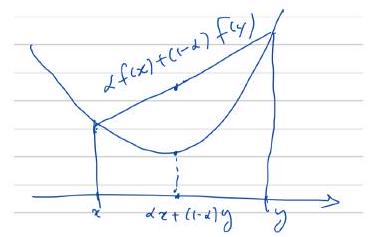
  1. \(f\) is called convex if for any \(x, y \in C\) and \(\alpha \in[0,1]\)

\[ f(\alpha x+(1-\alpha) y) \leq \alpha f(x)+(1-\alpha) f(y) \]

  1. \(f\) is called strictly convex if for any \(x \neq y \in C\) and \(\alpha \in(0,1)\) :

\[ f(\alpha x+(1-\alpha) y)<\alpha f(x)+(1-\alpha) f(y) \]

  1. A function \(f\) is said to be (strictly) concave if \(-f\) is (strictly) convex.

We also have the next diagram for convex function definition.

image

Lemma 6

If \(f(x)\) is differentiable on \(\mathbb{R}^{n}\), then \(f(x)\) is convex if and only if

\[ f(x) \geq f(y)+\nabla f(y) \cdot(x-y), \forall x, y \in \mathbb{R}^{n} \]

Based on the lemma, we can first have the next new diagram for convex functions.

image

Proof. Let \(z=\alpha x+(1-\alpha) y, 0 \leq \alpha \leq 1, \forall x, y \in \mathbb{R}^{n}\), we have these next two Taylor expansion:

\[\begin{split} \begin{aligned} &f(x) \geq f(z)+\nabla f(z)(x-z) \\ &f(y) \geq f(z)+\nabla f(z)(y-z) \end{aligned} \end{split}\]

Then we have

\[\begin{split} \begin{aligned} & \alpha f(x)+(1-\alpha) f(y) \\ \geq & f(z)+\nabla f(z)[\alpha(x-z)+(1-\alpha)(y-z)] \\ =& f(z) \\ =& f(\alpha x+(1-\alpha) y) . \end{aligned} \end{split}\]

Thus we have

\[ \alpha f(x)+(1-\alpha) f(y) \geq f(\alpha x+(1-\alpha) y) \]

This finishes the proof.

On the other hand: if \(f(x)\) is differentiable on \(\mathbb{R}^{n}\), then \(f(x) \geq f(y)+\) \(\nabla f(y) \cdot(x-y), \forall x, y \in \mathbb{R}^{n}\) if \(f(x)\) is convex.

Definition 3 (\(\lambda\)-strongly convex)

We say that \(f(x)\) is \(\lambda\)-strongly convex if

\[ f(x) \geq f(y)+\nabla f(y) \cdot(x-y)+\frac{\lambda}{2}\|x-y\|^{2}, \quad \forall x, y \in C \]

for some \(\lambda>0\).

Example. Consider \(f(x)=\|x\|^{2}\), then we have

\[ \frac{\partial f}{\partial x_{i}}=2 x_{i}, \nabla f=2 x \in R^{n} \]

So, we have

\[\begin{split} \begin{aligned} & f(x)-f(y)-\nabla f(y)(x-y) \\ =&\|x\|^{2}-\|y\|^{2}-2 y(x-y) \\ =&\|x\|^{2}-\|y\|^{2}-2 x y+2\|y\|^{2} \\ =&\|x\|^{2}-2 x y+\|y\|^{2} \\ =&\|x-y\|^{2} \\ =& \lambda\|x-y\|^{2}, \quad \lambda=2 . \end{aligned} \end{split}\]

Thus, \(f(x)=\|x\|^{2}\) is 2-strongly convex

Example. Actually, the loss function of the logistic regression model

\[ L(\theta)=-\log P(\theta) \]

is convex as a function of \(\theta\).

Furthermore, the loss function of the regularized logistic regression model

\[ L_{\lambda}(\theta)=-\log P(\theta)+\lambda\|\theta\|_{F}^{2}, \lambda>0 \]

is \(\lambda^{\prime}\)-strongly convex \(\left(\lambda^{\prime}\right.\) is related to \(\left.\lambda\right)\) as a function of \(\theta\).

We also have these following interesting properties of convex function.

Properties (basic properties of convex function)

1- If \(f(x), g(x)\) are both convex, then \(\alpha f(x)+\beta g(x)\) is also convex, if \(\alpha, \beta \geq 0\)

2- Linear function is both convex and concave. Here, \(f(x)\) is concave if and only if \(-f(x)\) is convex

3- If \(f(x)\) is a convex convex function on \(\mathbb{R}^{n}\), then \(g(y)=f(A y+b)\) is a convex function on \(\mathbb{R}^{m}\). Here \(A \in \mathbb{R}^{m \times n}\) and \(b \in \mathbb{R}^{m}\).

4- If \(g(x)\) is a convex function on \(\mathbb{R}^{n}\), and the function \(f(u)\) is convex function on \(\mathbb{R}\) and non-decreasing, then the composite function \(f \circ g(x)=f(g(x))\) is convex.

On the Convergence of GD

For the next optimization problem

\[ \min _{x \in \mathbb{R}^{n}} f(x) \]

We assume that \(f(x)\) is convex. Then we say that \(x^{*}\) is a minimizer if \(f\left(x^{*}\right)=\) \(\min _{x \in \mathbb{R}^{n}} f(x) .\)

Let recall that, for minimizer \(x^{*}\) we have

\[ \nabla f\left(x^{*}\right)=0 \]

Then we have the next tw properties of minimizer for convex functions:

  1. If \(f(x) \geq c_{0}\), for some \(c_{0} \in \mathbb{R}\), then we have

\[\arg \min f \neq \emptyset\]

  1. If \(f(x)\) is \(\lambda\)-strongly convex, then \(f(x)\) has a unique minimizer, namely, there exists a unique \(x^{*} \in \mathbb{R}^{n}\) such that

\[ f\left(x^{*}\right)=\min _{x \in \mathbb{R}^{n}} f(x) \]

To investigate the convergence of gradient descent method, let recall the gradient descent method:

Algorithm 3

For \(t = 1,2,\cdots\)

\[ \quad x_{t+1} = x_t - \eta_t \nabla f(x_t) \]

EndFor

where \(\eta_t\) is the stepsize / learning rate

Assumption

We make the following assumptions

1- \(f(x)\) is \(\lambda\)-strongly convex for some \(\lambda>0\). Recall the definition, we have

\[ f(x) \geq f(y)+\nabla f(y) \cdot(x-y)+\frac{\lambda}{2}\|x-y\|^{2} \]

then note \(x^{*}=\arg \min f(x)\). Then we have

  • Take \(y=x^{*}\), this leads to

\[ f(x) \geq f\left(x^{*}\right)+\frac{\lambda}{2}\|x-y\|^{2} \]

  • Take \(x=x^{*}\), this leads to

\[ 0 \geq f\left(x^{*}\right)-f(y) \geq \nabla f(y) \cdot\left(x^{*}-y\right)+\frac{\lambda}{2}\left\|x^{*}-y\right\|^{2} \]

which means that

\[ \nabla f(x) \cdot\left(x-x^{*}\right) \geq \frac{\lambda}{2}\left\|x-x^{*}\right\|^{2} \]

2- \(\nabla f\) is Lipschitz for some \(L>0\), i.e.,

\[ \|\nabla f(x)-\nabla f(y)\| \leq L\|x-y\|, \forall x, y \]

Thus, we have the next theorem about the convergence of gradient descent method.

Theorem 1

For Algorithm 3, if \(f(x)\) is \(\lambda\)-strongly convex and \(\nabla f\) is Lipschitz for some \(L>0\), then

\[ \left\|x_{t}-x^{*}\right\|^{2} \leq \alpha^{t}\left\|x_{0}-x^{*}\right\|^{2} \]

if \(0<\eta_{t} \leq \eta_{0}=\frac{\lambda}{2 L^{2}}\) and \(\alpha=1-\frac{\lambda^{2}}{4 L^{2}}<1.\)

Proof. If we minus any \(x \in \mathbb{R}^{n}\), we can only get:

\[ x_{t+1}-x=x_{t}-\eta_{t} \nabla f\left(x_{t}\right)-x \]

If we take \(L^{2}\) norm for both side, we get:

\[ \left\|x_{t+1}-x\right\|^{2}=\left\|x_{t}-\eta_{t} \nabla f\left(x_{t}\right)-x\right\|^{2} \]

So we have the following inequality and take \(x=x^{*}\) :

\(\left\|x_{t+1}-x^{*}\right\|^{2}=\left\|x_{t}-\eta_{t} \nabla f\left(x_{t}\right)-x^{*}\right\|^{2}\)

\(=\left\|x_{t}-x^{*}\right\|^{2}-2 \eta_{t} \nabla f\left(x_{t}\right)^{\top}\left(x_{t}-x^{*}\right)+\eta_{t}^{2}\left\|\nabla f\left(x_{t}\right)-\nabla f\left(x^{*}\right)\right\|^{2}\)

\(\leq\left\|x_{t}-x^{*}\right\|^{2}-\eta_{t} \lambda\left\|x_{t}-x^{*}\right\|^{2}+\eta_{t}^{2} L^{2}\left\|x_{t}-x^{*}\right\|^{2} \quad(\lambda-\) strongly convex and Lipschitz \()\)

\(\leq\left(1-\eta_{t} \lambda+\eta_{t}^{2} L^{2}\right)\left\|x_{t}-x^{*}\right\|\).

So, if \(\eta_{t} \leq \frac{\lambda}{2 L^{2}}\), then \(\alpha=\left(1-\eta_{t} \lambda+\eta_{t}^{2} L^{2}\right) \leq 1-\frac{\lambda^{2}}{4 L^{2}}<1\), which finishes the proof.

Some issues on GD:

  • \(\nabla f\left(x_{t}\right)\) is very expensive to compete.

  • GD does not yield generalization accuracy.

The stochastic gradient descent (SGD) method which we will discuss in the next section will focus on these two issues.