Contents

Preliminary Quiz

For Penn State student, access quiz here

import ipywidgets as widgets

Queation 1

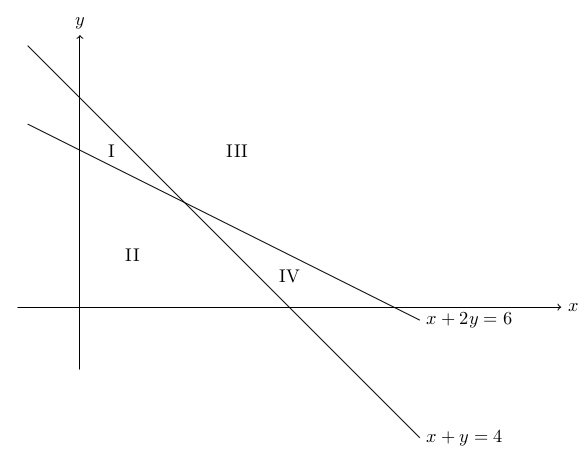
image

Consider the feasible region given by the following inequalities. whose boundary lines are graphed above.

\[\begin{split} x+2y \geq 6 \\ x+y \geq 4 \\ x \geq 0 \\ y \geq 0 \\ \end{split}\]

Which ONE of the following labels best indicate the feasible region described above?

Show answer

Answer: III

Question 2

Let

\[ f(x) = x_1^2+x_3^2+x_3^4, p =(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}) , g(t)=f(x+tp) \]

where \(t\) is a scalar variable. Find \(g^{'}(0)\) at \(x=(1,1,1)\)

Show answer

Answer:

\[ 3\sqrt{3} \]

Question 3

Determine the global maximum and global minimum of the function

\[ f(x) = x^3-3x^2+5 \]

on the interval \([-2,3]\)

Show answer

Answer:

Global maximum is 5; global minimum is -15.

Question 4

Find the global minimizer and the global minimum value of the function

\[ f(x,y)=(x-2)^2+y^2+2(y-4)^2+2x^2+2xy+4y-16x+1. \]

That is, determine the point \((x_0,y_0)\) which yields the global minimum value,

Show answer

Answer: \(x_0 = 3\), \(y_0 = 1\)

\(f_{min} = 1\)

Problem 5

Which of the following matrices has an inverse?

\[\begin{split} \begin{bmatrix} 3&4 \\ 6&8 \\ \end{bmatrix} \end{split}\]
\[\begin{split} \begin{bmatrix} 0&-4 \\ 0&10 \\ \end{bmatrix} \end{split}\]
\[\begin{split} \begin{bmatrix} 4&-10 \\ 2&5 \\ \end{bmatrix} \end{split}\]
\[\begin{split} \begin{bmatrix} 1&4 \\ 0&3 \\ \end{bmatrix} \end{split}\]
\[\begin{split} \begin{bmatrix} 0&0 \\ 5&7 \\ \end{bmatrix} \end{split}\]
Show answer

Answer:

\[\begin{split} \begin{bmatrix} 1&4 \\ 0&3 \\ \end{bmatrix} \end{split}\]

Question 6

Let

\[\begin{split} A=\left( \begin{matrix} 1&-1&0\\ -1&2&-1\\ 0&-1&1 \end{matrix} \right) \end{split}\]

Compute the eigenvalues of \(A\)

Show answer

Answer:

1,0,3

Question 7

Let

\[\begin{split} a= \begin{bmatrix} 1\\ 1\\ 1\\ 1 \end{bmatrix} \in R^4 \end{split}\]

and \(A=aa^T\)

Find the eigenvalues and corresponding eigenvectors of \(A\)

Write out solution.

Show answer
\[\begin{split} \lambda =4 , x = \begin{bmatrix} 1\\ 1\\ 1\\ 1 \end{bmatrix} \end{split}\]
\[\begin{split} \lambda = 0, x = \begin{bmatrix}1\\-1\\0\\0 \end{bmatrix} \begin{bmatrix}1\\0\\-1\\0\end{bmatrix} \begin{bmatrix}1\\0\\0\\-1\end{bmatrix} \end{split}\]

Question 8

How would you code \(ax^2\) in python?

Show answer

\(3*x**2\)

Question 9

When writing in python, what will be the output after the following statements?

m = 92
n = 35
print(m > n)

True
Show answer

True

Question 10

NumPy is a library for the Python programming language which provides support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays. For example,

x = np.array([1, 2, 3])

will set x to a vector array with components (1, 2, 3). To utilize the above array function as listed, what do you need to do prior to using it?

Show answer

import numpy as np