from IPython.display import IFrame

IFrame(src="https://cdnapisec.kaltura.com/p/2356971/sp/235697100/embedIframeJs/uiconf_id/41416911/partner_id/2356971?iframeembed=true&playerId=kaltura_player&entry_id=1_6e90qr52&flashvars[streamerType]=auto&amp;flashvars[localizationCode]=en&amp;flashvars[leadWithHTML5]=true&amp;flashvars[sideBarContainer.plugin]=true&amp;flashvars[sideBarContainer.position]=left&amp;flashvars[sideBarContainer.clickToClose]=true&amp;flashvars[chapters.plugin]=true&amp;flashvars[chapters.layout]=vertical&amp;flashvars[chapters.thumbnailRotator]=false&amp;flashvars[streamSelector.plugin]=true&amp;flashvars[EmbedPlayer.SpinnerTarget]=videoHolder&amp;flashvars[dualScreen.plugin]=true&amp;flashvars[hotspots.plugin]=1&amp;flashvars[Kaltura.addCrossoriginToIframe]=true&amp;&wid=1_joaa51cu" ,width='800', height='500')

-->

Introduction to Python and Pytorch¶

Grader: Boqian Shen

Email: Boqian.shen@kaust.edu

Anaconda
Python
Pytorch
Jupyter Notebook
Use Jupyter Notebook to do programing with Python and Pytorch (reading material):

Example 1: Plot the curve of a function

Example 2: Root finding

Example 3: Solve Ax=b

Example 4: Calculate the derivative of a function

Example 5: Find the maximum and minimum of a list of numbers

1. Anaconda¶

Anaconda is a free and open-source distribution of the Python and R programming languages for scientific computing (data science, machine learning applications, large-scale data processing, predictive analytics, etc.), that aims to simplify package management and deployment. Package versions are managed by the package management system conda. The Anaconda distribution includes data-science packages suitable for Windows, Linux, and MacOS.

Install Anaconda (Recommend: Python 3.7 version, Command Line version) from 
https://www.anaconda.com/distribution/

2. Python¶

Python is a high-level, general-purpose programming language. For examples:

(1) Create a calculator (calculate tips, annual tax, monthly expense…)

(2) Solve mathematical problems (root finding, plot some functions, solve Ax=b…)

(3) Say “hello” to Machine Learning

(4) Data mining (find all the online information which includes your name…)

(5) Create personal webpage

(6) Design games

…

Python is very powerful! If you want to do something with Python, just Google it!

Note that if you have already downloaded Anaconda, Python will be automaticly installed.

3. PyTorch¶

Pytorch is an open source machine learning library, used for applications such as computer vision and natural language processing. It is developed by Facebook’s AI Research lab. It is free and open-source software.

Install Pytorch from https://pytorch.org/ , or use 

conda install pytorch torchvision -c pytorch  (Mac User)

conda install pytorch torchvision cpuonly -c pytorch  (Windows and Linux Users)    

4. Jupyter Notebook¶

Jupyter Notebook is a web-based interactive computational environment for creating Jupyter notebook documents. A Jupyter Notebook document contains an ordered list of input/output “cells” which can contain code, text (using Markdown), mathematics, plots and rich media, usually ending with the “.ipynb” extension.

A Jupyter Notebook can be converted to a number of open standard output formats (HTML, presentation slides, LaTeX, PDF, ReStructuredText, Markdown, Python) through "Download As" in the web interface, via the nbconvert library or "jupyter nbconvert" command line interface in a shell. (Student can do their hw with Jupyter notebook, then submit a .ipynb file. Then the grader can run the code)

e.g. This is an exapmle of Markdown cell with “Tex” equation.

\[f(x)=x^2\]

# e.g. This is an example of Python code cell.
2/8

# A line started with a pound sign means it is a comment line

0.25

# How to use Pytorch
import torch

# We can initialize a matrix as a pytorch tensor:
A = torch.tensor([[1,2,3],[4,5,6],[7,8,9]]) 
print('A is', A)

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
<ipython-input-3-9279f38d9c4d> in <module>
      1 # How to use Pytorch
----> 2 import torch
      3 
      4 # We can initialize a matrix as a pytorch tensor:
      5 A = torch.tensor([[1,2,3],[4,5,6],[7,8,9]])

ModuleNotFoundError: No module named 'torch'

Install Jupyter Notebook from https://jupyter.org/install, or use
conda install -c conda-forge notebook

Run Jupyter Notebook:
Step 1: type "jupyter notebook" in command line
Step 2: Find the link shows in the command line
Step 3: Open the link with your browser

5. Use Jupyter Notebook to do programing with Python and Pytorch¶

Part A: Basic Python Language¶

Arithmetic¶

Like every programming language, Python is a good calculator. Run the block of code below to make sure the answer is right!

8 + 6*2*3 -1 + 2/3

43.666666666666664

Question: How to calculate the power of a number?

In python, m ** n means \(m^n\)

3 ** 2
2 ** 3
4 ** 2

if 4>2:
    print(4)

Pay attention: the rule of indent!

x=3
    y=3
# The two "spaces" at the front of "y=3" are unexpected indent
# Check the indent rule of python: https://docs.python.org/2.0/ref/indentation.html

  File "<ipython-input-10-ea97276566de>", line 2
    y=3
    ^
IndentationError: unexpected indent

Variables¶

So you just had a big meal, and now you need to calculate the tip.

meal = 220.00
tip_percent = 0.15
meal * tip_percent

33.0

“meal” and “tip_percent” are not numbers, they are called variables.

In Python variables are like buckets (dump trucks?). You can put anything you want in them. Just give them a name and then you can use them.

meal = 220
tip_percent = 0.15
tip = meal * tip_percent

However, a variable will not be printed automatically.

print(tip)

33.0

# a string is defined with 'your string' or "your string"
x = 'Hello World!'
print(type(x))  # will print the variable type
print(x)  #will print the actual variable value

<class 'str'>
Hello World!

x = 1
print(type(x))

<class 'int'>

tip_words = 'The tips should be:'
tip = 220 * 0.15

# One can connect two string by using the sigh +
tip_words_total = tip_words + str(tip) #str(tip) converts a number to a string 

print(tip_words_total)

The tips should be:33.0

if-elif-else¶

# if-elif-else
x = 0 
if x > 0:
    print('x is strictly positive')
elif x < 0:
    print('x is strictly negative')
else:
    print('x is zero')

x is zero

for loop and list¶

for i in range(7):
    print(i)

print('New')

x = [1,0,2,8,3,5,2]
# Given a list x
for i in range(len(x)):
    print('The ',i,'th element in list x is:', x[i])


for i in x:
    print(i)

0
1
2
3
4
5
6
New
The  0 th element in list x is: 1
The  1 th element in list x is: 0
The  2 th element in list x is: 2
The  3 th element in list x is: 8
The  4 th element in list x is: 3
The  5 th element in list x is: 5
The  6 th element in list x is: 2
1
0
2
8
3
5
2

Logical operators¶

# Logical operators
# bool type:  "True" (=1), "False" (=0)
x = True
y = False

print('type of x is:',type(x)) #will print out variable type

print('x and y is:',x and y) # boolean operator and

print('x or y is:',x or y)  # boolean operator or

print('not x is:',not x) # boolean operator not

type of x is: <class 'bool'>
x and y is: False
x or y is: True
not x is: False

Comparsion operators¶

# Comparsion operator: the output is bool type
x = 10
y = 12

# Output: x > y (is x greater than y?)
print('x > y is',x>y)

# Output: x < y (is x less than y?)
print('x < y is',x<y)

#Output: x == y (is x equal to y?)
print('x == y is',x==y)

#Output: x!=y (is x not equal to y?)
print('x != y is',x!=y)

#There is also 'greater than or equal' >=  less than or equal' <=
# Output: x >= y is False
print('x >= y is',x>=y)

# Output: x <= y is True
print('x <= y is',x<=y)

x > y is False
x < y is True
x == y is False
x != y is True
x >= y is False
x <= y is True

Question: what is the difference between “x =10” and “x == 10”

x=10 is an assignment setting the variable x equal to 10
x==10 is a comparison (output true false) answering the question, Is x equal to 10?

import numpy as np
# Am example combines the commands introduced above together
# Pay more attention the indent rule
x = np.random.randint(0,11,size=10)  #defines a vector of integers of length 10, it calls numpy package

for i in x:
    print(i)
    
print('The length of the list is: ',len(x))

# Count how many numbers are bigger than 5 and how many numbers are less than 5 and how many numbers are equal to 5
# We define and initialize the variables
count_bigger = 0
count_smaller = 0
count_equal = 0

for i in range(len(x)):
    if x[i]>5:
        count_bigger = count_bigger + 1
    elif x[i]<5:
        count_smaller = count_smaller + 1
    else:   # all other
        count_equal = count_equal + 1
        
print('number bigger than 5: ',count_bigger)
print('number less than 5: ', count_smaller)
print('number equal to 5: ', count_equal)

#Check by seeing if count_equal == len(x)-(count_bigger + count_smaller)
print(count_equal == len(x)- (count_bigger+count_smaller))  # boolen True/False

7
4
0
1
2
5
4
8
1
6
The length of the list is:  10
number bigger than 5:  3
number less than 5:  6
number equal to 5:  1
True

Part B: Some examples¶

# you can use many Python packages by importing them. Check the reference: 
#https://docs.python.org/3/reference/import.html

# NEED TO IMPORT numpy as np as notes use "np" to call numpy package, 
# numpy is a fundamental package for scientific computing with Python.
import numpy as np  

import matplotlib.pyplot as plt 
# matplotlib is a plotting library for the Python programming language 

import torch 
# import Pytorch

Example 1¶

Plot the curve of a funtion

#The above "header" was done using a "markdown" cell and markdown header designator

import torch
import numpy as np
import matplotlib.pyplot as plt
# Define a function f(x) = x^2
def f(x):
    return x ** 2 
def g(x):
    return x ** 2 + 1000
#generate a linear space with torch.linspace(start, end, steps)
x=torch.linspace(-100, 100, 10)

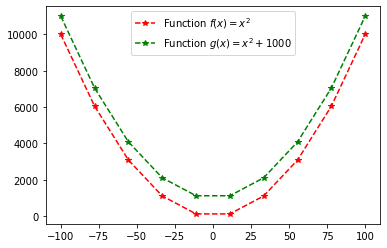
plt.plot(x, f(x), '*--r', label='Function $f(x)=x^2$') #point is * and color is red and label embedded LaTeX
plt.plot(x, g(x), '*--g', label='Function $g(x)=x^2 + 1000$')

plt.legend()

# plt.figure()
# plt.plot(x, g(x), '*--r', label='Function g(x)=x')
# plt.legend()

<matplotlib.legend.Legend at 0x122090668>

Exercise 1¶

Plot the curve of function \( f(x) = x^3 - x, x \in [-1,1]. \)

=================================================================================================================

Example 2¶

Find the roots of a function

\(f(x) = x-2\)¶

#Above cell is a 'markdown' cell written  $f(x) = x-2$ which is embedded LaTeX

from scipy.optimize import fsolve
def f(x):
    return x - 2

# We us root = fsolve(function, initial guess) to find ONE root of a function
# If a function has multiple roots, the output 'root' will be the one closest to 'initial guess'
x0 = fsolve(f, 0)
print('The root is:', x0)

The root is: [2.]

\(h(x) = x + 2 cos(x),~~ x \in[-4,4].\)¶

#Again, above cell is a 'markdown' cell written $h(x)=x+2\cos(x),~~x\in[-4,4]$ which is embedded LaTeX

import numpy as np
def h(x):
    return x + 2 * np.cos(x)
x0 = fsolve(h, 1)
print('The root is:', x0)
x = np.linspace(-4, 4, 1000)

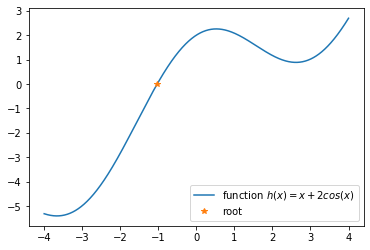
plt.plot(x, h(x),'-', label='function $h(x)=x + 2 cos(x)$')
plt.plot(x0, h(x0), '*',label='root') # draw the solution point on the curve
plt.legend()

The root is: [-1.02986653]

<matplotlib.legend.Legend at 0x10237fef28>

Exercise 2¶

(1) Find the two roots of the function¶

\( f(x) = 2x^2 - x - 1 , x \in [-1,2]. \)

(2) Plot the curve of the function \(f(x)\) defined in (1) and mark all the roots on the curve.¶

=================================================================================================================

Example 3¶

create A vector and a matrix (generally use tensors in Pytorch) and solve \(Ax=b\)

\( A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}, \quad\quad b=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \)

where \(x=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}\) are unknown variables.¶

Remark: it is equivalent to solve¶

\( 1 * x_1 + 2 * x_2 + 3 * x_3 = 1\\ 4 * x_1 + 5 * x_2 + 6 * x_3 = 2\\ 7 * x_1 + 8 * x_2 + 9 * x_3 = 3\\ \)

import torch
import numpy as np

# We can initialize a matrix as a Pytorch tensor: [[row 1],[row 2],[row 3]]
A = torch.tensor([[1,2,3],[4,5,6],[7,8,9]],dtype=torch.float32) # the type of data is torch.float32
print('A is', A)


# Print an empty line.
print('\n') 

# We can initialize a column vector as a pytorch tensor:
b = torch.tensor([[1],[2],[3]],dtype=torch.float32) 
print('b is', b)

A is tensor([[1., 2., 3.],
        [4., 5., 6.],
        [7., 8., 9.]])


b is tensor([[1.],
        [2.],
        [3.]])

# We use LU factorization to solve Ax=b by calling torch.solve(b,A)
x, LU =torch.solve(b,A) 
# the ouput gives you the solution x and LU, which contains L and U factors for LU factorization of A
print('x is', x)

x is tensor([[ 9.9341e-09],
        [-1.9868e-08],
        [ 3.3333e-01]])

# We can also initialize a zeroed tensor and check the data type of the tensor
c1 = torch.zeros([2,2])
print('c1 is:', c1) 
print('Type of c1:', c1.dtype) 

# Print an empty line.
print('\n') 

# Note that the default type of such a tensor is a 32-bit float.
c2 = torch.zeros([2,2], dtype=torch.int32)
print('c2 is', c2)
print('Type of c2:', c2.dtype)

c1 is: tensor([[0., 0.],
        [0., 0.]])
Type of c1: torch.float32


c2 is tensor([[0, 0],
        [0, 0]], dtype=torch.int32)
Type of c2: torch.int32

# some basic operations

# plus
c = c1 + 1
print(c)

c[0,0] = c[0,0]+1
print(c)

tensor([[1., 1.],
        [1., 1.]])
tensor([[2., 1.],
        [1., 1.]])

# multiply
c = c * 2
print(c)

print('\n')

# multiplication of a matrix and a vector (generally two size-matched tensors)

d = torch.tensor([[1],[2]],dtype=torch.float32) 
print(d)
c = torch.mm(c,d)
print(c)

tensor([[4., 2.],
        [2., 2.]])


tensor([[1.],
        [2.]])
tensor([[8.],
        [6.]])

Exercise 3.1¶

Given \(P=\begin{bmatrix} 1 & 2 \\ 3 & 4\end{bmatrix}\), investigate the two different multiplications \(P*P\) and \(torch.mm(P,P)\).

Exercise 3.2¶

Given \( A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}, \quad\quad b=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}. \)

Solve \(A^2 x = b\)¶

=================================================================================================================

Example 4¶

Calculate the derivate of \((xy)^2\) at \(x=1, y=2\) w.r.t \(x\).

We wish to calculate \( \dfrac{\partial f}{\partial y}|_{x=1,y=2}\) where \(f(x,y)=(xy)^2\)

\(\dfrac{\partial f}{\partial y} = 2xy^2\), thus \(\dfrac{\partial f(1,2)}{\partial y} = 2 \cdot 1 \cdot (2^2)=8\)

# In order to calculate the gradient with respect to a tensor, we should set the requires_grad flag to True.
x = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([2.0])

# By default, requires_grad is set to False if possible.
print('x requires_grad?', x.requires_grad)
print('y requires_grad?', y.requires_grad)

z = (x*y)**2
print('z.requires_grad?', z.requires_grad)


# Calculate the derivative of out w.r.t. x. Automatically applies the chain rule as needed.
grad = torch.autograd.grad(outputs=z, inputs=x) 
print(grad)

x requires_grad? True
y requires_grad? False
z.requires_grad? True
(tensor([8.]),)

Exercise 4¶

Calculate the derivative of \(x^2+y^2+(xy)^3\) at \(x=1,y=2\) w.r.t \(y\).

=================================================================================================================

Example 5¶

Define a function to find the maximum of three numbers \(a,~b,~c\). Test your code and print the maximum of the three numbers, where \(a=\sqrt{2},~ b=\frac{4}{3},~ c=0.5e\)

# Define a function
# def is a keyword, which means you are defining a function
# f_max is the name of the function
# (a,b,c) are the input of the function
# return some_value gives you the output of the function
# Pay attention on the indent rules
def f_max(a,b,c): 
    max_value = a
    if b> max_value:
        max_value = b
    if c > max_value:
        max_value=c
    return max_value

a = 2 ** 0.5
b = 4/3
c = 0.5 * np.exp(1)
print('a=',a)
print('b=',b)
print('c=',c)

# call function f_max with input a=2 ** 0.5, b = 4/3, c = 0.5 * np.exp(1)
# The function will return the maximum value of a,b,c
print('The maximum of a,b,c is:',f_max(a,b,c))

a= 1.4142135623730951
b= 1.3333333333333333
c= 1.3591409142295225
The maximum of a,b,c is: 1.4142135623730951

Exercise 5.1¶

Define a function to find the minimum of three numbers \(a,~b,~c\). Test your code and print the minimum of the three numbers, where \(a=\sqrt{2},~ b=\frac{4}{3},~ c=0.5e\)

Exercise 5.2¶

Define a function to find the maximum and minimum of a sequence with n numbers.

Hint: x = np.random.randint(a,b,size=n) can randomly generate n numbers (saved in a row vector x ) and each number is between a and b.

Exercise 5.3¶

Define a function to sort a sequence with n numbers in ascending order.

=================================================================================================================

Course background and introduction

Preliminary Quiz

Deep Learning Web Course

Introduction to Python and Pytorch¶

1. Anaconda¶

2. Python¶

3. PyTorch¶

4. Jupyter Notebook¶

5. Use Jupyter Notebook to do programing with Python and Pytorch¶

Part A: Basic Python Language¶

Arithmetic¶

Variables¶

if-elif-else¶

for loop and list¶

Logical operators¶

Comparsion operators¶

Part B: Some examples¶

Example 1¶

Exercise 1¶

Example 2¶

\(f(x) = x-2\)¶

\(h(x) = x + 2 cos(x),~~ x \in[-4,4].\)¶

Exercise 2¶

(1) Find the two roots of the function¶

(2) Plot the curve of the function \(f(x)\) defined in (1) and mark all the roots on the curve.¶

Example 3¶

where \(x=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}\) are unknown variables.¶

Remark: it is equivalent to solve¶

Exercise 3.1¶

Exercise 3.2¶

Solve \(A^2 x = b\)¶

Example 4¶

Exercise 4¶

Example 5¶

Exercise 5.1¶

Exercise 5.2¶

Exercise 5.3¶