Research Results
My research ranges from pure theoretical analysis, basic algorithmic development to practical applications.
I mainly work on numerical methods for partial differential equations (PDEs) and big data, such as finite element, multi-grid (MG), domain decomposition (DD) methods and deep neural networks, for their theoretical analysis, algorithmic development, and practical applications. Theoretical elegance and practical usefulness can go together, and the design and analysis of algorithms can be beautiful. Theory is the soul of what I do, and practical needs are what motivate me. In all my work, I try to strike a balance between rigor and practicality.
Examples of my better known works include the Bramble-Pasciak-Xu preconditioner (a basic algorithm for solving elliptic PDEs) and the Hiptmair-Xu preconditioner (an effective Maxwell solver which was featured in a 2008 report by the U.S. Department of Energy as one of the top 10 breakthroughs in computational science in recent years). I developed the framework and theory of the Method of Subspace Corrections that have been widely used in the literature for the design and analysis of iterative methods and later established the Xu-Zikatanov identity, giving the optimal theory for these methods. I also designed the Morley-Wang-Xu (MWX) element, which is the only known class of finite elements universally constructed for elliptic partial differential equations of any order in any spatial dimension.
In recent years, I have spent much time research of deep learning, focusing on approximation theory, deep learning model, training algorithms, and application to numerical PDEs. In particular, we have observed close conneciton between ReLU-DNN and linear FEM, CNN and multigrid method and developed MgNet that can outperform the corresponding CNN for various applications such as image classification.
Examples:
-
Multigrid Algorithms and Subspace Corrections
-
Bramble-Pasciak-Xu preconditioner (BPX)
-
Hiptmair-Xu preconditioner (HX)
-
Representative works on the convergence theories for MG and DD methods
-
Convergence estimates for multigrid algorithms without regularity assumptions, J. Bramble, J. Pasciak, J. Wang, and J. Xu, Math. Comp., 57, 23--45, 1991
-
Convergence estimates for product iterative methods with applications to domain decomposition, J. Bramble, J. Pasciak, J. Wang, and J. Xu, Math. Comp., 57, 1--21, 1991
-
Novel Finite Element Algorithms and Theories
-
The algorithms and theories of optimal solver and asymptotically exact a posteriori error estimators for PDEs discretized on unstructured grids;
-
Asymptotically exact a posteriori error estimators. I.
Grids with superconvergence, R. Bank, and J. Xu, SIAM J. Numer.
Anal., 41, 2294--2312, 2003
-
Asymptotically exact a posteriori error estimators. II.
General unstructured grids, R. Bank, and J. Xu, SIAM J. Numer.
Anal., 41, 2313--2332, 2003
-
The two-grid discretization methods;
-
A novel two-grid method for semilinear elliptic equations
, J. Xu, SIAM J. Sci. Comput., 15, 231 -- 237, 1994
-
Two-grid discretization techniques for linear and
nonlinear PDEs, J. Xu, SIAM J. Numer. Anal., 33, 1759--1777,
1996
-
Extended Galerkin Methods
-
An extended Galerkin analysis in finite element exterior calculus, Hong, Q., Li, Y. and Xu, J., Mathematics of Computation, 91(335), pp.1077-1106, 2022.
-
New discontinuous Galerkin algorithms and analysis for linear elasticity with symmetric stress tensor, Hong, Q., Hu, J., Ma, L. and Xu, J., Numerische Mathematik, 149(3), pp.645-678, 2021.
-
Uniform Stability and Error Analysis for Some
Discontinuous Galerkin Methods, Hong, Q. and Xu, J, Journal of Computational Mathematics, 39(2), 2021.
-
An extended Galerkin analysis for elliptic problems, Hong, Q., Wu, S. and Xu, J., Science China Mathematics, 64, pp.2141-2158, 2021.
-
A unified study of continuous and discontinuous Galerkin methods, Hong, Q., Wang, F., Wu, S. and Xu, J., Science China Mathematics, 62, pp.1-32, 2019.
-
The only known canonical construction of finite element family for any order of elliptic PDEs in any spatial dimensions;
-
Minimal Finite Element Spaces for $2m$-th-order Partial
Differential Equations in $R^n$, M. Wang, and J. Xu, Math.
Comp., 82, 24 -- 43, 2013.
-
Nonconforming Finite Element Spaces for $2m$-th Order Partial Differential Equations on $R^n$ Simplicial Grids when $m=n+1$, S. Wu, and J.
Xu, Math. Comp.88 (316), 531-551, 2019.
-
$\mathcal{P}^m$ Interior Penalty Nonconforming Finite Element Methods
for $2m$-th Order PDEs in $R^n$, S. Wu, and J. Xu, arXiv preprint arXiv:1710.0 7678, 2017.
-
Multiphysics problems
-
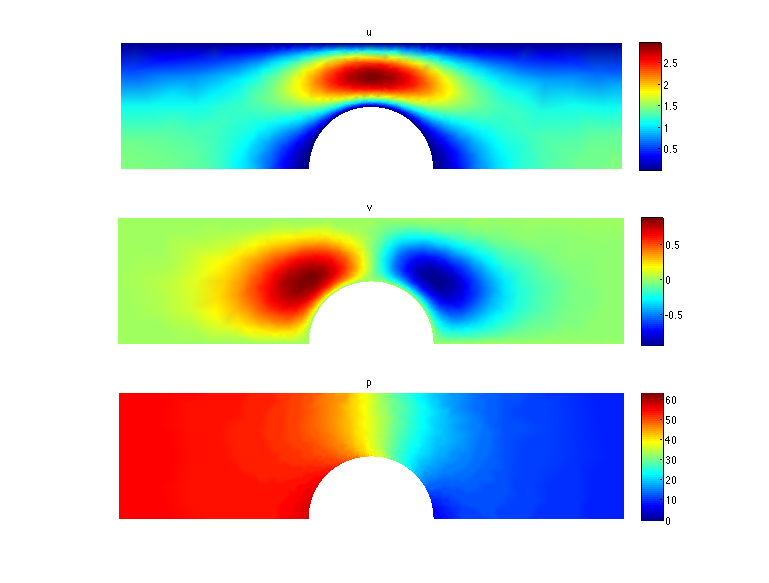
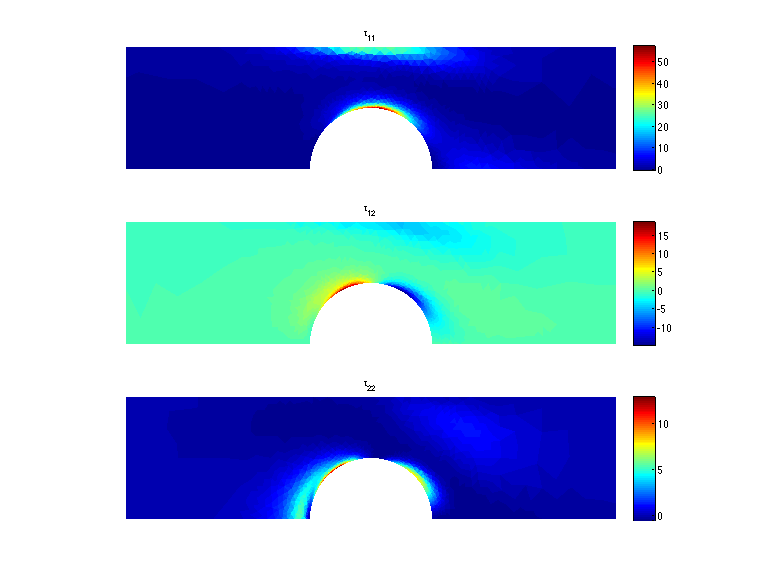
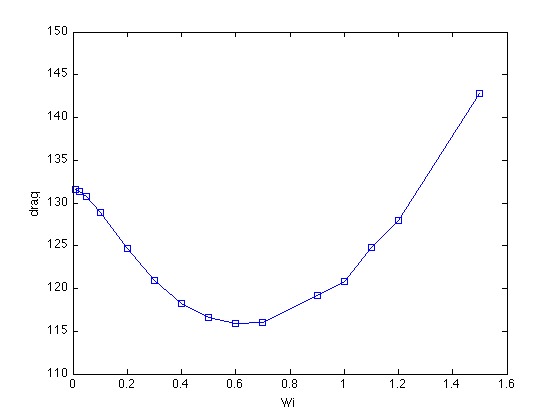
The new algorithm and theory for non-Newtonian flows with high Weissengberg numbers;
-
New formulations, positivity preserving discretizations
and stability analysis for non-Newtonian flow models, Y.-J.
Lee, and J. Xu, Comput. Methods Appl. Mech. Engrg. (195)
1180--1206, 2006
-
Global existence, uniqueness and optimal solvers of
discretized viscoelastic flow models, Y.-J. Lee, J. Xu
and C. Zhang, M3AS, 21(8), 1713--1732, 2001
-
The monolithic discretization and robust solvers for fluid-structure interaction (FSI);
-
Full Eulerian Finite Element Method of a Phase Field Model
for Fluid-structure Interaction Problem
, P. Sun, J. Xu, and L. Zhang, Comput. Fluids, 90, 1 -- 8, 2014
-
Modeling and simulation for fluid and rotating structure
interaction
, K. Yang, P. Sun, L. Wang, J. Xu, and L. Zhang,
Comput. Methods in Appl. Mech. Eng., 311, 788 -- 814, 2016
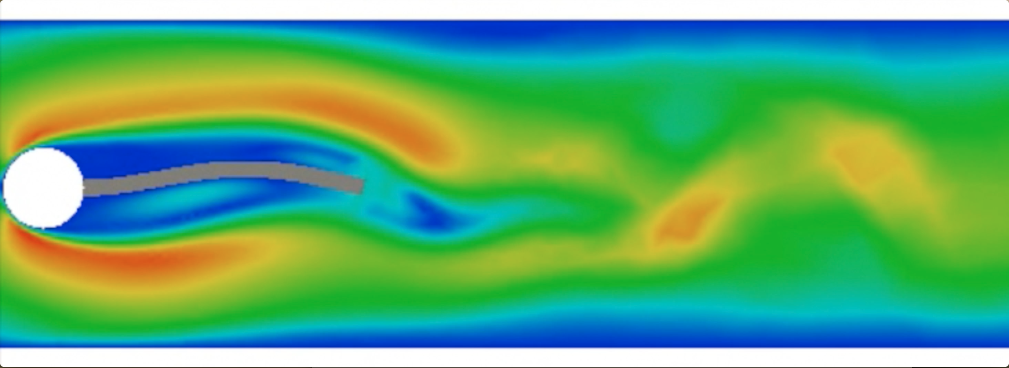
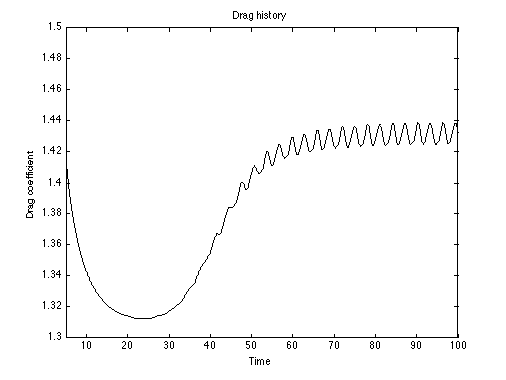
Turek Fluid-Structure Interaction Benchmark
|

Moving mesh for real hydroelectric generator
|
-
The structure-preserving discretization and robust solvers for magnetohydrodynamics (MHD);
-
Stable Finite Element Methods Preserving $\nabla \cdot
B = 0$ Exactly for MHD Models, K. Hu, Y.
Ma, and J. Xu, Numer. Math., 135(2), 371--396, 2017
-
Robust Preconditioners for Incompressible MHD Models
, Y. Ma, K. Hu, X. Hu, and J. Xu, J. Comput. Phys., 316, 721 -- 746, 2016
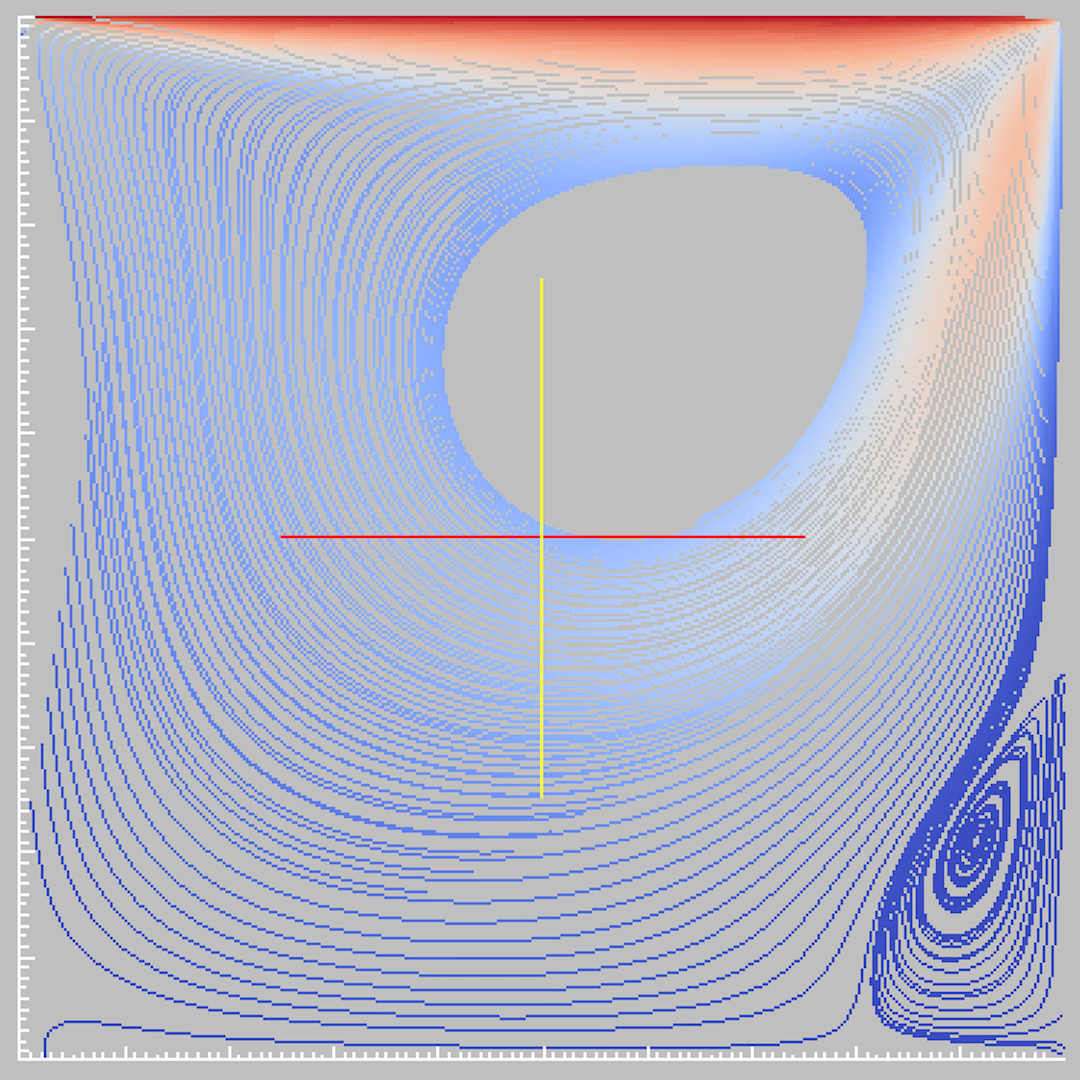
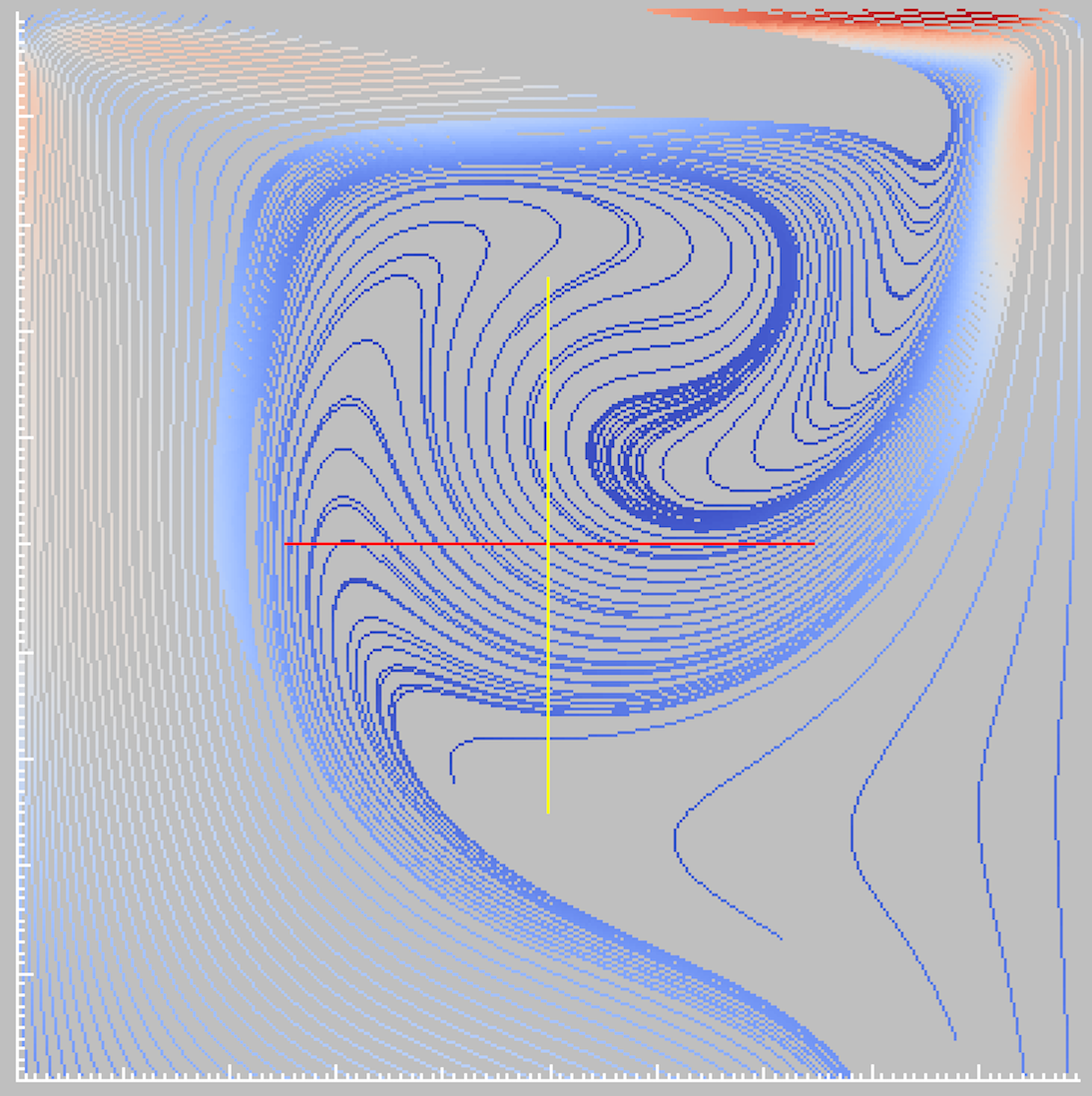
Lid-driven cavity, Re=400, Rm=400: (left) stream line of the
velocity; (right) distribution of the total magnetic field
Lid-driven cavity, Re=400, Rm=400: number of iterations
|
-
Analysis of the numerical schemes for phase field models and interface problems;
-
On the Stability and Accuracy of Partially and Fully
Implicit Schemes for Phase Field Modeling
, J. Xu, Y. Li, and S. Wu, Computer Methods in Applied Mechanics and Engineering 345: 826-853, 2019
-
Multiphase Allen-Cahn and Cahn-Hilliard models and their
discretizations with the effect of pairwise surface
tensions, S. Wu, and J. Xu, J. Comput. Phys., 343, 10--32, 2017
-
High-order Extended Finite Element Methods for Solving
Interface Problems, F. Wang, Y. Xiao, and J. Xu, Computer Methods in Applied Mechanics and Engineering 364: 112964, 2020
-
Deep Learning
-
Neural Networks Approximation Theory
-
ReLU deep neural networks from the hierarchical basis perspective, He, J., Li, L. and Xu, J., Computers & Mathematics with Applications, 120, pp.105-114, 2022.
-
Sharp bounds on the approximation rates, metric entropy, and n-widths of shallow neural networks, Siegel, J.W. and Xu, J, Foundations of Computational Mathematics, pp.1-57., 2022.
-
Uniform approximation rates and metric entropy of shallow neural networks, Ma, L., Siegel, J.W. and Xu, J, Research in the Mathematical Sciences, 9(3) p.46, 2022.
-
Approximation properties of deep ReLU CNNs, He, J., Li, L. and Xu, J., Research in the Mathematical Sciences, 9(3), p.38, 2022.
-
Approximation rates for neural networks with general activation functions, Siegel, J.W. and Xu, J., Neural Networks, 128, pp.313-321, 2020.
-
Optimal convergence rates for the orthogonal greedy algorithm, Siegel, J.W. and Xu, J., IEEE Transactions on Information Theory,2022
-
High-order approximation rates for shallow neural networks with cosine and ReLU^k activation functions, Siegel, J.W. and Xu, J., Applied and Computational Harmonic Analysis, 58, pp.1-26, 2022.
-
Training algorithms
-
Make $\ell_1$ Regularization Effective in Training Sparse CNN,He, J., Jia, X., Xu, J., Zhang, L. and Zhao, L., Computational Optimization and Applications, 77(1), pp.163-182, 2020.
-
Greedy Training Algorithms for Neural Networks and Applications to PDEs, Siegel, J.W., Hong, Q., Jin, X., Hao, W. and Xu, J., arXiv preprint arXiv:2107.04466, 2021.
-
Extended Regularized Dual Averaging Methods for Stochastic Optimization, J. Siegel and J. Xu, arXiv:1904.02316, 2019
-
Finite Neuron Method
-
Meta-mgnet: Meta multigrid networks for solving parameterized partial differential equations, Chen, Y., Dong, B. and Xu, J., Journal of Computational Physics, 455, p.110996, 2022.
-
Finite neuron method and convergence analysis, Xu, J., Communications in Computational Physics, 28(5), pp.1707-1745, 2020.
-
On the activation function dependence of the spectral bias of neural networks, Hong, Q., Tan, Q., Siegel, J.W. and Xu, J., arXiv preprint arXiv:2208.04924, 2022.
-
Deep Learning Models
-
CNNs with Compact Activation Function, Wang, J., Xu, J. and Zhu, J., In Computational Science-ICCS 2022: 22nd International Conference, London, UK, June 21-23, 2022, Proceedings, Part II (pp. 319-327). Cham: Springer International Publishing. 2022, June.
-
MgNet: A Unified Framework of Multigrid and Convolutional Neural Network, J. He and J. Xu, Sci. China Math., 62, 2019
-
ReLU Deep Neural Networks and Linear Finite Elements, J. He, L. Li, J. Xu and C. Zheng, J. Comput. Math., 2019
-
Applications
-
A machine learning method correlating pulse pressure wave data with pregnancy, Chen, J., Huang, H., Hao, W. and Xu, J., International journal for numerical methods in biomedical engineering, 36(1), p.e3272, 2020.
-
FV-MgNet: Fully Connected V-cycle MgNet for Interpretable Time Series Forecasting, J. Zhu, J. He, L. Zhang, and J. Xu, arXiv preprint arXiv:2302.00962, 2023.
|